- on: June 15, 2024
- in: NeurIPS
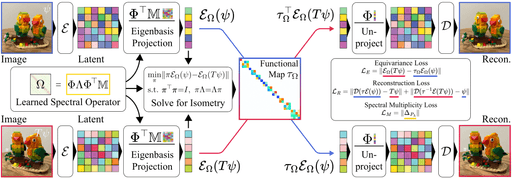
Neural Isometries: Taming Transformations for Equivariant ML
@inproceedings{mitchel2024neuralisometries,
title = { Neural Isometries: Taming Transformations for Equivariant ML },
author = { Mitchel, Tommy and
Taylor, Mike and
Sitzmann, Vincent },
year = { 2024 },
booktitle = { NeurIPS },
}Real-world geometry and 3D vision tasks are replete with challenging symmetries that defy tractable analytical expression. In this paper, we introduce Neural Isometries, an autoencoder framework which learns to map the observation space to a general-purpose latent space wherein encodings are related by isometries whenever their corresponding observations are geometrically related in world space. Specifically, we regularize the latent space such that maps between encodings preserve a learned inner product and commute with a learned functional operator, in the same manner as rigid-body transformations commute with the Laplacian. This approach forms an effective backbone for self-supervised representation learning, and we demonstrate that a simple off-the-shelf equivariant network operating in the pre-trained latent space can achieve results on par with meticulously-engineered, handcrafted networks designed to handle complex, nonlinear symmetries. Furthermore, isometric maps capture information about the respective transformations in world space, and we show that this allows us to regress camera poses directly from the coefficients of the maps between encodings of adjacent views of a scene.